AdamFranco.com

Adam December 5th, 2012

Filed under: Computers and Technology , Software

Tags: cartography, geography, Google Earth, KML, maps, motorcycles, OpenStreetMap, OSM, python

In the process of taking up motorcycling this summer I also gained an additional hobby: scouring maps and travel guides to find the roads that would be most fun to ride. While I’ve had great times on dirt roads through farmland and wide open highways, there just isn’t anything that compares to the thrill of leaning through the corners on a winding road.

While I’ve had some good successes in locating roads by map (such as Tracy Road), one of the shortcomings of a map is the tight curves you can really lean into tend to be below the resolution for many maps. Atlases and electronic maps like Google Earth allow you to zoom in, but then there is the problem of finding the gems in the sea of data. What I realized I needed was a way to highlight just the most curvy roads so that I would know where to explore next.

For those less familiar with the intersection of cartography and software, the electronic mapping systems of the world (your Garmin/TomTom GPS, Google Earth, MapQuest, etc) have sequences of thousands of coordinates that linked together define the paths of roads across the surface of the earth.

While most of these systems use proprietary data sets, a service called Open Street Map (OSM) is a community driven project that anyone can add and edit — a Wikipedia for cartographic data. In some parts of the world the Open Street Map has better coverage than any commercial providers; in the US the original data was imported from the public domain USGS TIGER data set and has then been expanded and improved by the community. I’ve known this data was available for a long time, but it was only last week I realized that it would be possible to search through the coordinates that make up road-paths to analyze their geometry rather than just their position.

I can get the raw data from the Open Street Map for the path of every road, but how to determine which ones are the most twisty? At the beginning I tried a strategies such as calculating the ratio of distance traveled on a road versus the distance between the start and end points. Unfortunately all of these methods had situations that confused the algorithms (such as circular roads) or didn’t distinguish between fun curves and boring broad changes of direction that would only be exciting at far beyond the speed limit. What I eventually came up with is a process of calculating the radius of curvature at every segment of every road and then adding up the length of the most curvy segments to get a total distance spent turning. The twistier the road, the more time spent turning.

I’ll get back to more of the details in a bit, but I ended up writing a small program that reads through the Open Street Map data and spits out KML (Google Earth) files that highlight just the twisty roads. This program is called curvature.py and is available on Github here: https://github.com/adamfranco/curvature/wiki

When running curvature.py you can pass a variety of options that allow you to highlight the roads you are most interested in. For example if you live in the flat Midwest you can pass it a low curvature threshold to try to locate roads that have any curves. Give it a medium threshold and the output can help you find a more interesting route to work. Similarly if you want to find just the most absolutely crazy-curvy roads in a region give it a high threshold to filter out wheat from the chaff.

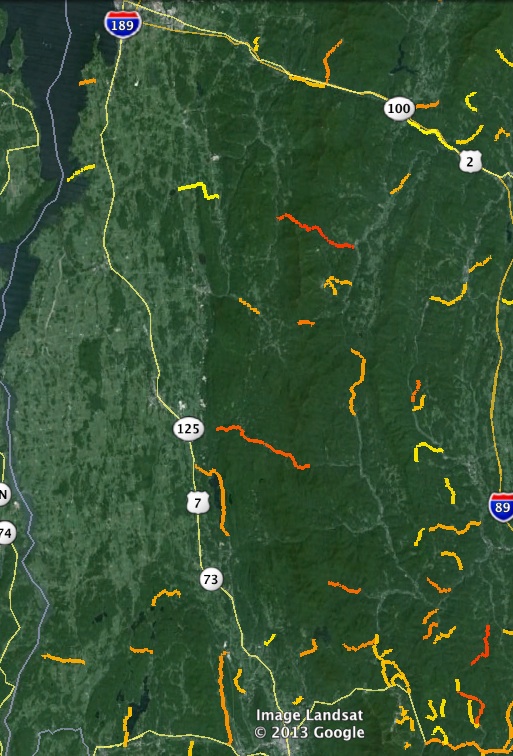
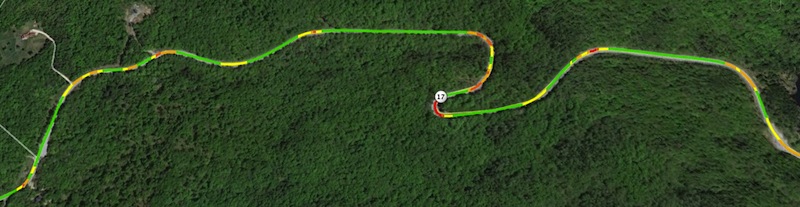
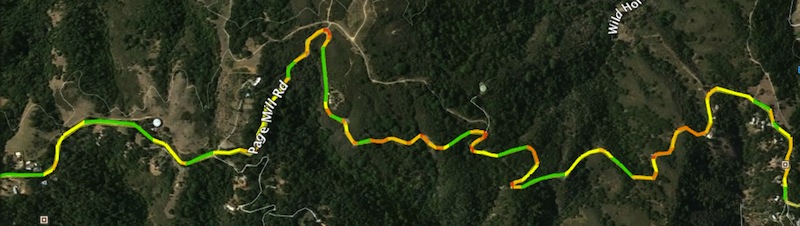
With the --colorize option, KML files will be generated with each road segment color-coded to match its curve-radius. Green segments are above the threshold considered “straight”, while yellow are broad curves, orange tighter, and red tightest:

More about calculating the curvature

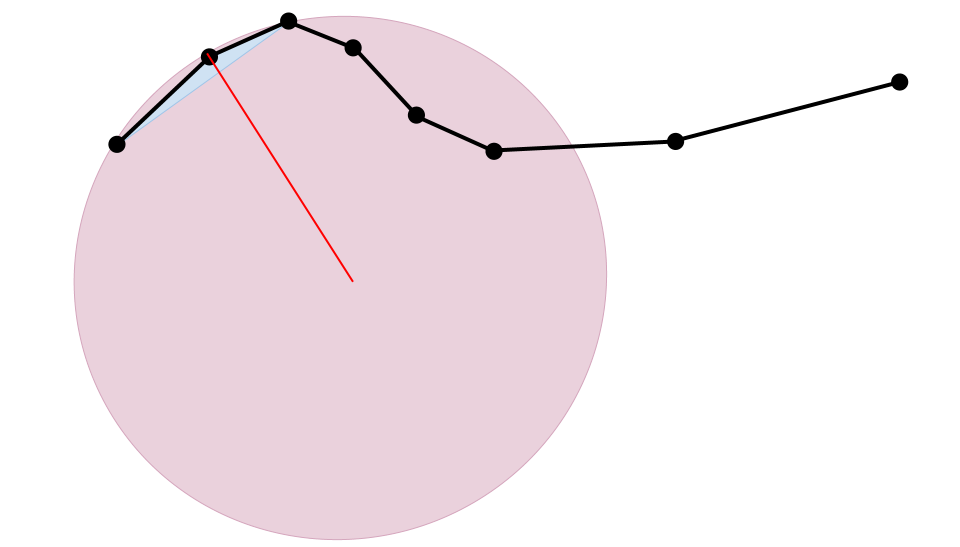
Each way (road) is made up of a sequence of points defined as a pair of latitude and longitude values. Each sequence of three points makes up a triangle where two of the sides are road segments with a hypotenuse between the 1st and 3rd points. Since we have the latitude and longitude of each point we can easily calculate the distances between them, but figuring out what the curvature of the road is at this set of points is a little tricky. Since the points aren’t evenly spaced the angle between the three points doesn’t tell us anything. Instead, we must go back to the geometric relationship that says for every triangle there is a circumcircle that intersects its three points. Using the equations for the circumcircle, we can plug in the distances between the three points and come up with the radius of that circle. That circle’s radius corresponds to the radius of the road’s curve at the middle of the three points.

Here is a video explaining the process:

Using Curvature
The Curvature Examples page shows a number of examples and provides links to KML files that you can open in Google Earth. If you’d like to just view curvature KML files that I’ve generated, you can find them at: http://www2.adamfranco.com/curvature/kml/

• Comments(2)